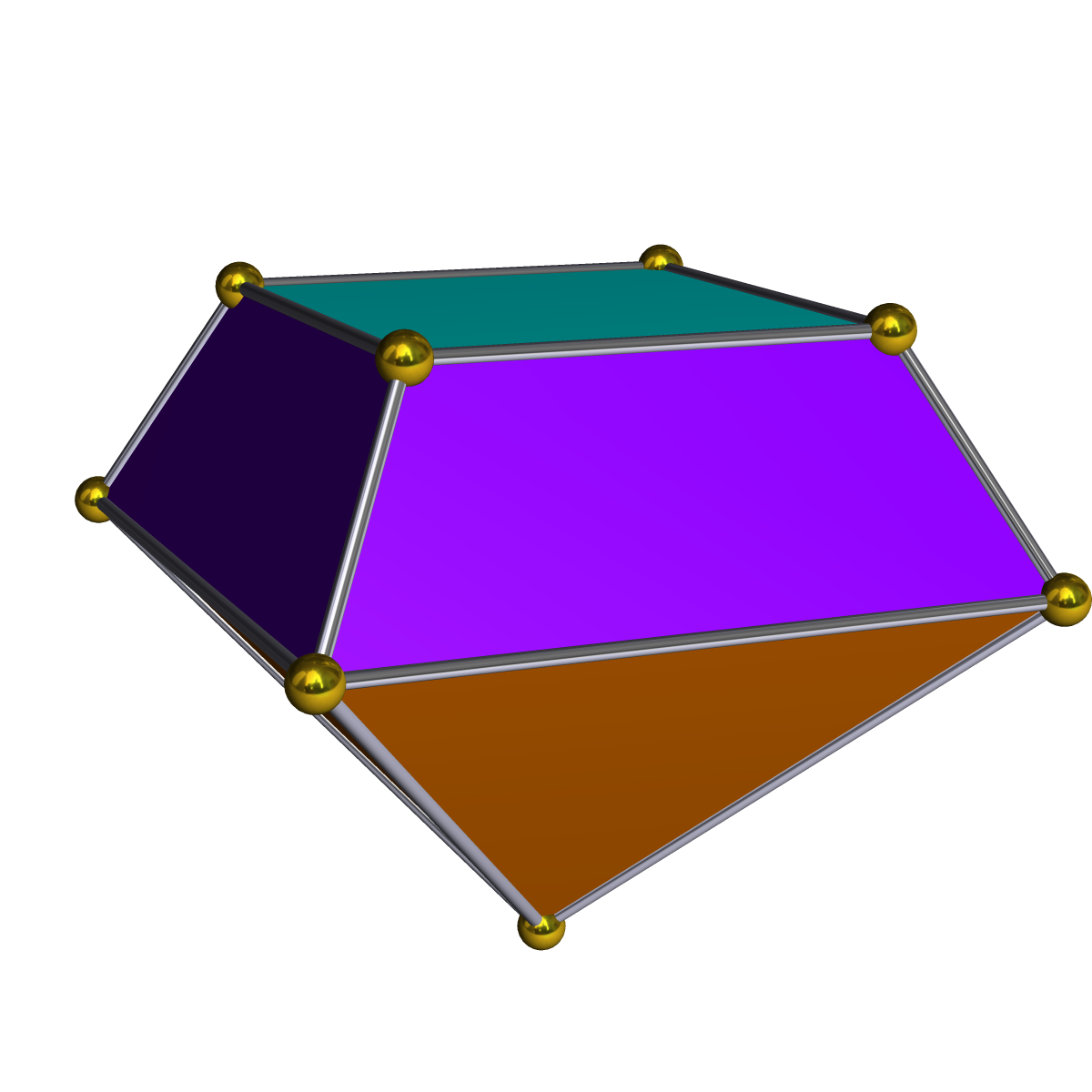
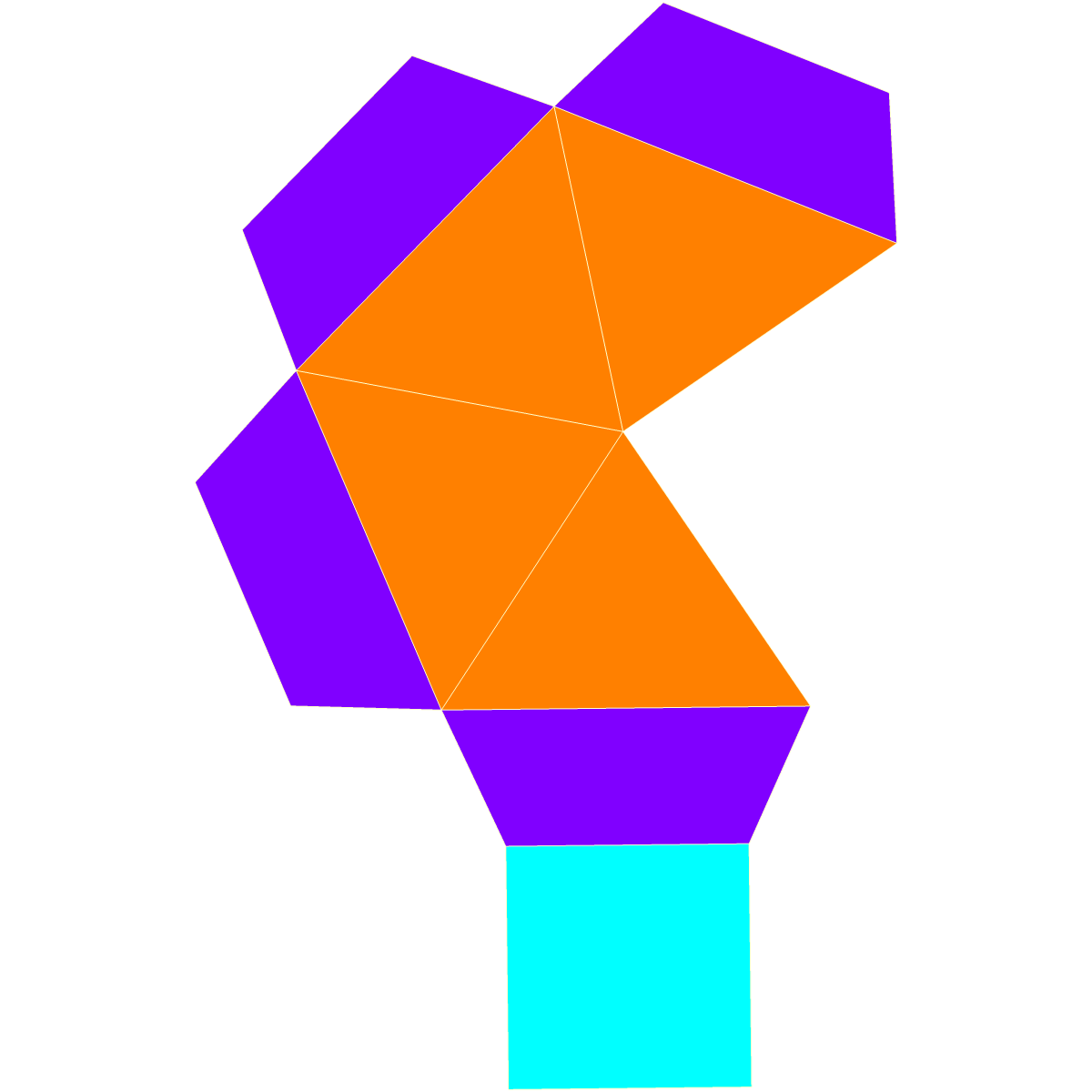
늘린 사각뿔

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 구성
3. 성질
- 3.1. 측정값
- 3.2. 이면각
4. 쌍대다면체
5. 관련 다면체 및 벌집
- 5.1. 관련 다면체
참조

1. 개요

늘린 사각뿔은 정육면체의 한 면에 정사각뿔을 붙여서 만들 수 있는 다면체이다. 이 도형은 정삼각형 4개와 정사각형 5개로 총 9개의 면을 가지며, 3차원 대칭군 C₄ᵥ를 갖는다. 늘린 사각뿔의 높이, 표면적, 부피는 변의 길이에 따라 특정 수식으로 계산되며, 쌍대다면체는 9개의 면을 가진다. 또한 정사면체와 함께 공간 테셀레이션을 만들 수 있으며, 정육면체, 정사각뿔, 정삼각기둥뿔, 정오각기둥뿔, 쌍사각뿔기둥, 정사각뿔반기둥 등과 관련이 있다.

더 읽어볼만한 페이지

각뿔과 쌍각뿔 - 비틀어 늘린 쌍각뿔
비틀어 늘린 쌍각뿔은 n각 쌍뿔의 두 밑면 사이에 n각 엇각기둥을 추가하여 만들어지며, 밑면의 형태에 따라 종류가 나뉘고, 정삼각형으로만 이루어진 경우 델타다면체로 불린다.
각뿔과 쌍각뿔 - 육각뿔
육각뿔은 육각형 밑면과 삼각형 면으로 이루어진 뿔 모양의 다면체로, 7개의 꼭짓점, 12개의 모서리, 7개의 면을 가지며, 자기 쌍대 다면체이다.
자기쌍대 다면체 - 육각뿔
육각뿔은 육각형 밑면과 삼각형 면으로 이루어진 뿔 모양의 다면체로, 7개의 꼭짓점, 12개의 모서리, 7개의 면을 가지며, 자기 쌍대 다면체이다.
자기쌍대 다면체 - 오각뿔
오각뿔은 밑면이 오각형이고 한 점에서 만나는 5개의 삼각형으로 이루어진 다면체로, 밑면이 정오각형이고 높이가 밑면 중심에 수직인 경우 정오각뿔이라고 하며, 존슨의 다면체 중 하나로 다양한 분야에 응용된다.
존슨의 다면체 - 삼각쌍뿔
삼각쌍뿔은 6개의 정삼각형 면, 5개의 꼭짓점, 9개의 모서리를 가진 존슨 다면체이자 델타다면체로, 두 정사면체를 밑면끼리 결합한 형태이며, 분자 기하학, 색채 이론 등 다양한 분야에 응용된다.
존슨의 다면체 - 오각지붕
오각지붕은 5개의 정삼각형, 5개의 정사각형, 1개의 정오각형, 1개의 정십각형으로 이루어진 존슨의 다면체이며, 회전 대칭을 갖고, 다양한 다면체를 구성하는 데 사용된다.

늘린 사각뿔
개요
종류	존슨의 다면체
Johnson 번호	J8
구성 면	정사각형 5개, 정삼각형 4개
변의 수	16
꼭짓점의 수	9
대칭군	C4v
꼭짓점 배치	4(4^3), 1(3^4), 4(3^2.4^2)
쌍대	자신
성질	볼록 다면체
형태
면의 종류	삼각형 4개, 정사각형 5개
모서리 수	16개
꼭짓점 수	9개
대칭
대칭군	C4v, [4], (*44)
회전군	C4, [4]+, (44)
각도
삼각형-삼각형	109.47°
정사각형-정사각형	90°
삼각형-정사각형	144.74°
분류
종류	존슨의 다면체
Johnson 넘버	J7 - J8 - J9
Net
전개도
그림
늘린 사각뿔

2. 구성

늘린 사각뿔은 정육면체의 한 면에 정사각뿔을 붙여 만들 수 있다. 이를 통해 정삼각형 4개와 정사각형 5개, 총 9개의 면을 가진다.

3. 성질

늘린 사각뿔은 정사각뿔과 동일한 3차원 대칭군인 8차 순환군 $C_{4v}$ 를 갖는다. 이면각은 정사각뿔과 정육면체의 각도를 더하여 얻을 수 있다.

3. 1. 측정값

변의 길이가

a

인 늘린 사각뿔의 높이는 정사각뿔과 정육면체의 높이를 더하여 계산할 수 있다. 정육면체의 높이는 정육면체 한 변의 길이와 같고, 정사각뿔의 높이는

(1/\sqrt{2})a

이다. 따라서 늘린 사각쌍뿔의 높이는 다음과 같다.

:

a + \frac{1}{\sqrt{2}}a = \left(1 + \frac{\sqrt{2}}{2}\right)a \approx 1.707a.

표면적은 네 개의 정삼각형과 네 개의 정사각형의 면적을 모두 더하여 계산할 수 있다.

:

\left(5 + \sqrt{3}\right)a^2 \approx 6.732a^2.

부피는 정사각뿔과 정육면체로 잘라서 더하여 얻는다.

:

\left(1 + \frac{\sqrt{2}}{6}\right)a^3 \approx 1.236a^3.

측정값	공식
겉넓이	$S=(5+\sqrt{3})a^2$
부피	$V=\over{6}}a^3$

3. 2. 이면각

이면각 종류	각도
두 인접한 삼각형 사이	$\arccos(-1/3) \approx 109.47^\circ$
두 인접한 정사각형 사이	$\pi/2 = 90^\circ$
정사각형과 삼각형 사이	$\arctan \left(\sqrt{2}\right) + \frac{\pi}{2} \approx 144.74^\circ$

4. 쌍대다면체

늘린 사각뿔의 쌍대다면체는 면이 9개이다. 삼각형 4개, 정사각형 1개와 등변사다리꼴 4개로 이루어져 있다.

늘린 사각뿔의 쌍대	쌍대다면체의 전개도

5. 관련 다면체 및 벌집

늘린 사각뿔은 정사면체와 함께 정사면체-정팔면체 벌집과 유사한 공간 테셀레이션을 만들 수 있다.^[8]

5. 1. 관련 다면체

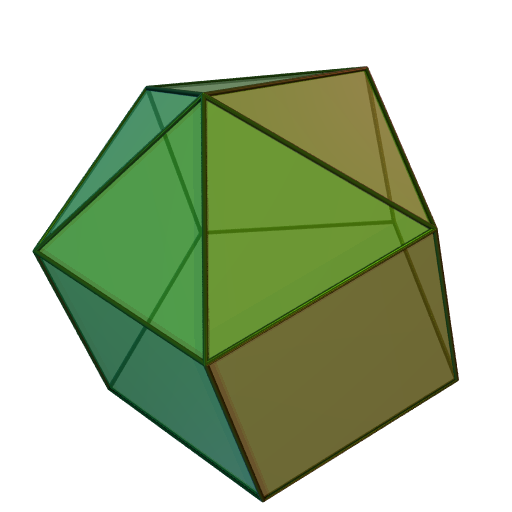
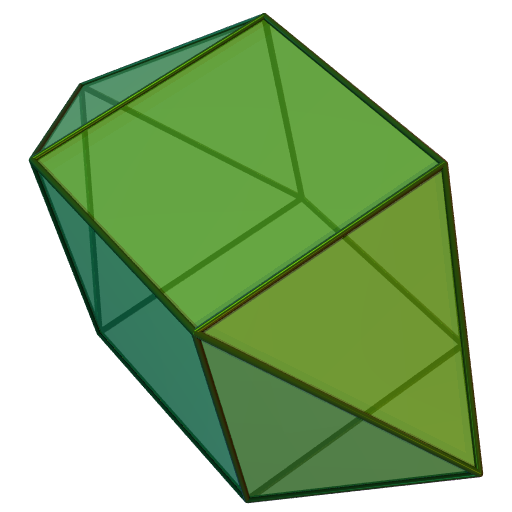
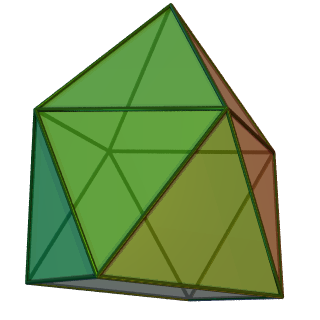
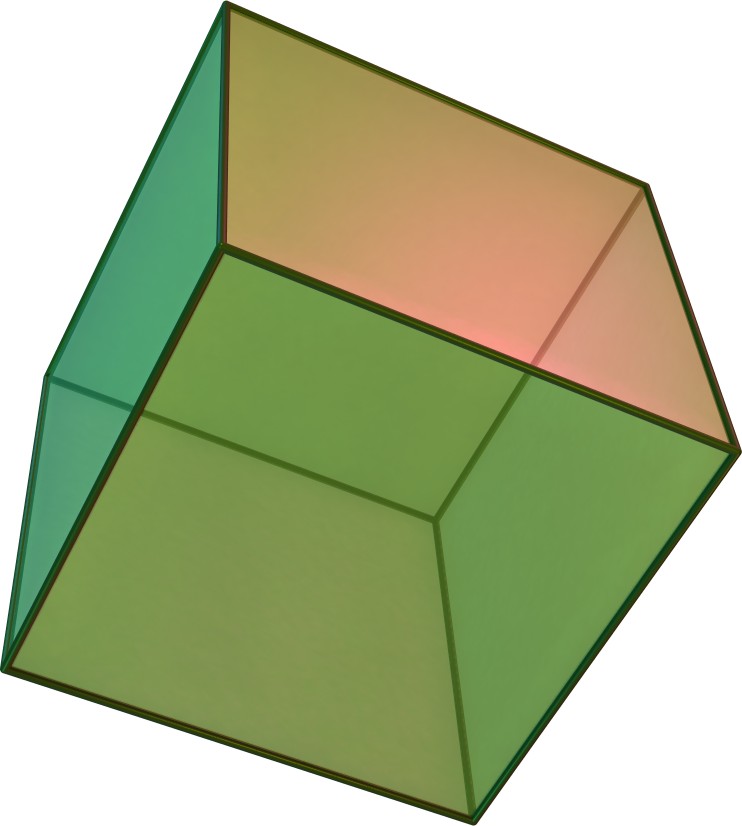
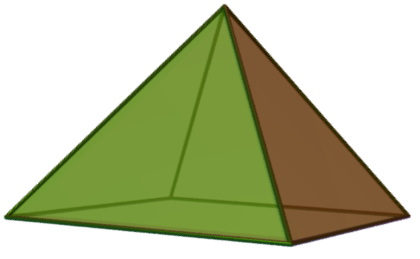
늘린 사각뿔과 관련된 다면체로는 정삼각기둥뿔(뿔의 각을 줄임), 정오각기둥뿔(뿔의 각을 늘림), 쌍사각뿔기둥(정사각뿔을 추가), 정사각뿔반기둥(45° 비틀기) 등이 있다. 또한, 늘린 사각뿔에서 정사각뿔을 제거하면 정육면체가 되고, 정육면체를 제거하면 정사각뿔이 된다.

5. 1. 1. 정다면체 기반

(정사각뿔을 제거)
(정육면체를 제거)